R TensorFlow Deep Neural Network

In the previous post I fitted a neural network to the cars_19 dataset using the neuralnet package.  In this post I am going to use TensorFlow to fit a deep neural network using the same data.

The main difference between the neuralnet package and TensorFlow is TensorFlow uses the adagrad optimizer by default whereas neuralnet uses rprop+  Adagrad is a modified stochastic gradient descent optimizer with a per-parameter learning rate.

The data which is all 2019 vehicles which are non pure electric (1253 vehicles) are summarized in previous posts below.

str(cars_19)
'data.frame':    1253 obs. of  12 variables:
 $ fuel_economy_combined: int  21 28 21 26 28 11 15 18 17 15 ...
 $ eng_disp             : num  3.5 1.8 4 2 2 8 6.2 6.2 6.2 6.2 ...
 $ num_cyl              : int  6 4 8 4 4 16 8 8 8 8 ...
 $ transmission         : Factor w/ 7 levels "A","AM","AMS",..: 3 2 6 3 6 3 6 6 6 5 ...
 $ num_gears            : int  9 6 8 7 8 7 8 8 8 7 ...
 $ air_aspired_method   : Factor w/ 5 levels "Naturally Aspirated",..: 4 4 4 4 4 4 3 1 3 3 ...
 $ regen_brake          : Factor w/ 3 levels "","Electrical Regen Brake",..: 2 1 1 1 1 1 1 1 1 1 ...
 $ batt_capacity_ah     : num  4.25 0 0 0 0 0 0 0 0 0 ...
 $ drive                : Factor w/ 5 levels "2-Wheel Drive, Front",..: 4 2 2 4 2 4 2 2 2 2 ...
 $ fuel_type            : Factor w/ 5 levels "Diesel, ultra low sulfur (15 ppm, maximum)",..: 4 3 3 5 3 4 4 4 4 4 ...
 $ cyl_deactivate       : Factor w/ 2 levels "N","Y": 1 1 1 1 1 2 1 2 2 1 ...
 $ variable_valve       : Factor w/ 2 levels "N","Y": 2 2 2 2 2 2 2 2 2 2 ...

To prepare the data to fit the neural network, TensorFlow requires categorical variables to be converted into a dense representation by using the column_embedding() function.

cols <- feature_columns(
  column_numeric(colnames(cars_19[c(2, 3, 5, 8)])),
  column_embedding(column_categorical_with_identity("transmission", num_buckets = 7),dimension = 1),
  column_embedding(column_categorical_with_identity("air_aspired_method", num_buckets = 5),dimension=1),
  column_embedding(column_categorical_with_identity("regen_brake", num_buckets = 3),dimension=1),
  column_embedding(column_categorical_with_identity("drive", num_buckets = 5),dimension=1),
  column_embedding(column_categorical_with_identity("fuel_type", num_buckets = 5),dimension=1),
  column_embedding(column_categorical_with_identity("cyl_deactivate", num_buckets = 2),dimension=1),
  column_embedding(column_categorical_with_identity("variable_valve", num_buckets = 2),dimension=1)
)

Similar to the neural network I fitted using neuralnet(), I am going to use two hidden layers with seven and three neurons respectively.

Train, evaluate, and predict:

#Create a deep neural network (DNN) estimator.
model <- dnn_regressor(hidden_units=c(7,3),feature_columns = cols)

set.seed(123)
indices <- sample(1:nrow(cars_19), size = 0.75 * nrow(cars_19))
train <- cars_19[indices, ]
test <- cars_19[-indices, ]

#train model
model %>% train(cars_19_input_fn(train, num_epochs = 1000))

#evaluate model
model %>% evaluate(cars_19_input_fn(test))

#predict
yhat <- model %>% predict(cars_19_input_fn(test))

yhat <- unlist(yhat)
y <- test$fuel_economy_combined

postResample(yhat, y)
RMSE  Rsquared       MAE 
1.9640173 0.8700275 1.4838347 

The results are similar to the other models and neuralnet().

I am going to look at the error rate in TensorBoard which is a visualization tool.  TensorBoard is great for visualizing TensorFlow graphs and for plotting quantitative metrics about the execution of the graph.  Below is the mean squared error at each iteration.  It stabilizes fairly quickly.  Next post I will get into TensorBoard in a lot more depth.

R Neural Network

In the previous four posts I have used multiple linear regression, decision trees, random forest, gradient boosting, and support vector machine to predict MPG for 2019 vehicles.   It was determined that svm produced the best model.  In this post I am going to use the neuralnet package to fit a neural network to the cars_19 dataset.

The raw data is located on the EPA government site.

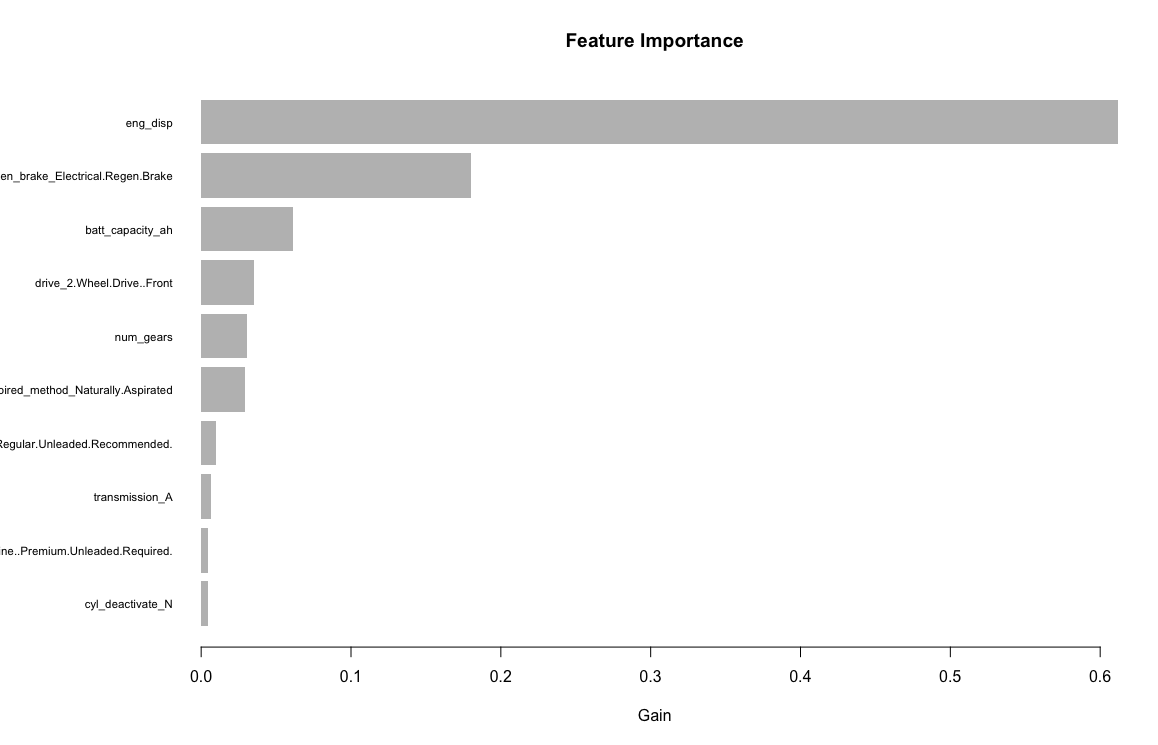
Similar to the other models, the variables/features I am using are: Engine displacement (size), number of cylinders, transmission type, number of gears, air inspired method, regenerative braking type, battery capacity Ah, drivetrain, fuel type, cylinder deactivate, and variable valve.  Unlike the other models, the neuralnet package does not handle factors so I will have to transform them into dummy variables.  After creating the dummy variables, I will be using 27 input variables.

The data which is all 2019 vehicles which are non pure electric (1253 vehicles) are summarized in previous posts below.

str(cars_19)
'data.frame':    1253 obs. of  12 variables:
 $ fuel_economy_combined: int  21 28 21 26 28 11 15 18 17 15 ...
 $ eng_disp             : num  3.5 1.8 4 2 2 8 6.2 6.2 6.2 6.2 ...
 $ num_cyl              : int  6 4 8 4 4 16 8 8 8 8 ...
 $ transmission         : Factor w/ 7 levels "A","AM","AMS",..: 3 2 6 3 6 3 6 6 6 5 ...
 $ num_gears            : int  9 6 8 7 8 7 8 8 8 7 ...
 $ air_aspired_method   : Factor w/ 5 levels "Naturally Aspirated",..: 4 4 4 4 4 4 3 1 3 3 ...
 $ regen_brake          : Factor w/ 3 levels "","Electrical Regen Brake",..: 2 1 1 1 1 1 1 1 1 1 ...
 $ batt_capacity_ah     : num  4.25 0 0 0 0 0 0 0 0 0 ...
 $ drive                : Factor w/ 5 levels "2-Wheel Drive, Front",..: 4 2 2 4 2 4 2 2 2 2 ...
 $ fuel_type            : Factor w/ 5 levels "Diesel, ultra low sulfur (15 ppm, maximum)",..: 4 3 3 5 3 4 4 4 4 4 ...
 $ cyl_deactivate       : Factor w/ 2 levels "N","Y": 1 1 1 1 1 2 1 2 2 1 ...
 $ variable_valve       : Factor w/ 2 levels "N","Y": 2 2 2 2 2 2 2 2 2 2 ...

First I need to normalize all the non-factor data and will use the min max method:

maxs <- apply(cars_19[, c(1:3, 5, 8)], 2, max)
mins <- apply(cars_19[, c(1:3, 5, 8)], 2, min)

scaled <- as.data.frame(scale(cars_19[, c(1:3, 5, 8)], center = mins, scale = maxs - mins))
tmp <- data.frame(scaled, cars_19[, c(4, 6, 7, 9:12)])

Neuralnet will not accept a formula like fuel_economy_combined ~. so I need to write out the full model.

n <- names(cars_19)
f <- as.formula(paste("fuel_economy_combined ~", paste(n[!n %in% "fuel_economy_combined"], collapse = " + ")))

Next I need to transform all of the factor variables into binary dummy variables.

m <- model.matrix(f, data = tmp)
m <- as.matrix(data.frame(m, tmp[, 1]))
colnames(m)[28] <- "fuel_economy_combined")

I am going to use the geometric pyramid rule to determine the amount of hidden layers and neurons for each layer.  The general rule of thumb is if the data is linearly separable, use one hidden layer and if it is non-linear use two hidden layers.  I am going to use two hidden layers as I already know the non-linear svm produced the best model.

r = (INP_num/OUT_num)^(1/3)
HID1_num = OUT_num*(r^2)   #number of neurons in the first hidden layer 
HID2_num = OUT_num*r          #number of neurons in the second hidden layer

This suggests I use two hidden layers with 9 neurons in the first layer and 3 neurons in the second layer. I originally fit the model with this combination but it turned out to overfit.  As this is just a suggestion, I found that two hidden layers with 7 and 3 neurons respectively produced the best neural network that did not overfit.

Now I am going to fit a neural network:

set.seed(123)
indices <- sample(1:nrow(cars_19), size = 0.75 * nrow(cars_19))
train <- m[indices,]
test <- m[-indices,]

n <- colnames(m)[2:28]
f <- as.formula(paste("fuel_economy_combined ~", paste(n[!n %in% "fuel_economy_combined"], collapse = " + ")))
m1_nn <- neuralnet(f,
                   data = train,
                   hidden = c(7,3),
                   linear.output = TRUE)

pred_nn <- predict(m1_nn, test)

yhat <-pred_nn * (max(cars_19$fuel_economy_combined) - min(cars_19$fuel_economy_combined)) + min(cars_19$fuel_economy_combined)
y <- test[, 28] * (max(cars_19$fuel_economy_combined) - min(cars_19$fuel_economy_combined)) +min(cars_19$fuel_economy_combined)

postResample(yhat, y)
     RMSE  Rsquared       MAE 
2.0036294 0.8688363 1.4894264 

I am going to run a 20 fold cross validation to estimate error better as these results are dependent on sample and initialization of the neural network.

set.seed(123)
stats <- NULL

for (i in 1:20) {
  indices <- sample(1:nrow(cars_19), size = 0.75 * nrow(cars_19))
  train_tmp <- m[indices, ]
  test_tmp <- m[-indices, ]
  
  nn_tmp <- neuralnet(f,
                      data = train_tmp,
                      hidden = c(7, 3),
                      linear.output = TRUE)
  
  pred_nn_tmp <- predict(nn_tmp, test_tmp)
  
  yhat <- pred_nn_tmp * (max(cars_19$fuel_economy_combined) - min(cars_19$fuel_economy_combined)) + min(cars_19$fuel_economy_combined)
  y <- test_tmp[, 28] * (max(cars_19$fuel_economy_combined) - min(cars_19$fuel_economy_combined)) + min(cars_19$fuel_economy_combined)
  stats_tmp <- postResample(yhat, y)
  stats <- rbind(stats, stats_tmp)
  cat(i, "\n")
}

mean(stats[, 1] ^ 2)      #avg mse  4.261991
mean(stats[, 1] ^ 2) ^ .5 #avg rmse 2.064459

colMeans(stats) #ignore rmse
#RMSE Rsquared      MAE 
#xxx  0.880502 1.466458 

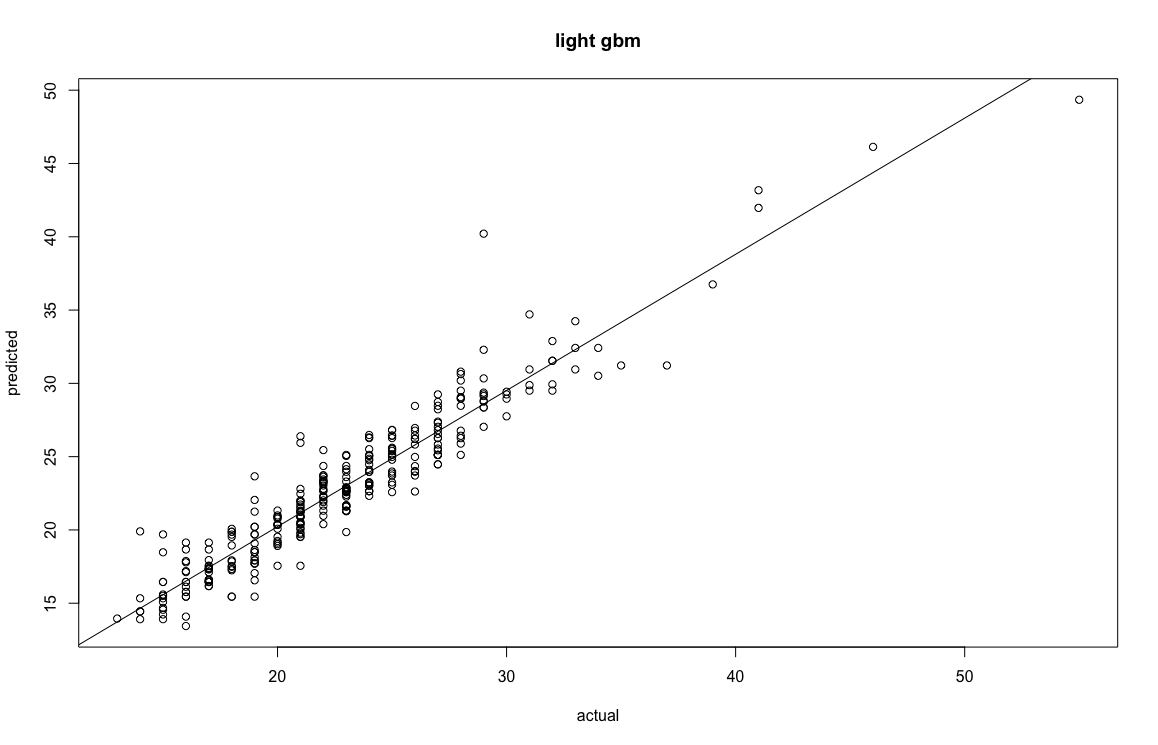
The neural network produces a RMSE of 2.06.

Comparison of RMSE:

svm = .93
gradient boosting = 1.8
random forest = 1.9
neural network = 2.06
decision tree = 2.49
mlr = 2.6

R Tensorflow Multiple Linear Regression

In the previous three posts I used multiple linear regression, decision trees, gradient boosting, and support vector machine to predict miles per gallon for 2019 vehicles.  It was determined that svm produced the best model.  In this post, I am going to run TensorFlow through R and fit a multiple linear regression model using the same data to predict MPG.

Part 1: Multiple Linear Regression using R

There are 1253 vehicles in the cars_19 dataset.  I am simply running mlr using Tensorflow for demonstrative purposes as using lm() in R is more efficient and more precise for such a small dataset.

TensorFlow uses an algorithm that is dependent upon convergence whereas R computes the closed form estimates of beta.  I will be using 11 features and an intercept so R will be inverting a 12 x 12 matrix which is not computationally expensive with today's technology.

The dataset below of 11 features contains 7 factor variables and 4 numeric variables. 

str(cars_19)
'data.frame':    1253 obs. of  12 variables:
 $ fuel_economy_combined: int  21 28 21 26 28 11 15 18 17 15 ...
 $ eng_disp             : num  3.5 1.8 4 2 2 8 6.2 6.2 6.2 6.2 ...
 $ num_cyl              : int  6 4 8 4 4 16 8 8 8 8 ...
 $ transmission         : Factor w/ 7 levels "A","AM","AMS",..: 3 2 6 3 6 3 6 6 6 5 ...
 $ num_gears            : int  9 6 8 7 8 7 8 8 8 7 ...
 $ air_aspired_method   : Factor w/ 5 levels "Naturally Aspirated",..: 4 4 4 4 4 4 3 1 3 3 ...
 $ regen_brake          : Factor w/ 3 levels "","Electrical Regen Brake",..: 2 1 1 1 1 1 1 1 1 1 ...
 $ batt_capacity_ah     : num  4.25 0 0 0 0 0 0 0 0 0 ...
 $ drive                : Factor w/ 5 levels "2-Wheel Drive, Front",..: 4 2 2 4 2 4 2 2 2 2 ...
 $ fuel_type            : Factor w/ 5 levels "Diesel, ultra low sulfur (15 ppm, maximum)",..: 4 3 3 5 3 4 4 4 4 4 ...
 $ cyl_deactivate       : Factor w/ 2 levels "N","Y": 1 1 1 1 1 2 1 2 2 1 ...
 $ variable_valve       : Factor w/ 2 levels "N","Y": 2 2 2 2 2 2 2 2 2 2 ...

The factors need to be transformed into a format TensorFlow can understand.

cols <- feature_columns(
  column_numeric(colnames(cars_19[c(2, 3, 5, 8)])),
  column_categorical_with_identity("transmission", num_buckets = 7),
  column_categorical_with_identity("air_aspired_method", num_buckets = 5),
  column_categorical_with_identity("regen_brake", num_buckets = 3),
  column_categorical_with_identity("drive", num_buckets = 5),
  column_categorical_with_identity("fuel_type", num_buckets = 5),
  column_categorical_with_identity("cyl_deactivate", num_buckets = 2),
  column_categorical_with_identity("variable_valve", num_buckets = 2)
  )

Create an input function:

#input_fn for a given subset of data
cars_19_input_fn <- function(data, num_epochs = 1) {
  input_fn(
    data,
    features = colnames(cars_19[c(2:12)]),
    response = "fuel_economy_combined",
    batch_size = 64,
    num_epochs = num_epochs
  )
}

Train, evaluate, predict:

model <- linear_regressor(feature_columns = cols)

set.seed(123)
indices <- sample(1:nrow(cars_19), size = 0.75 * nrow(cars_19))
train <- cars_19[indices, ]
test <- cars_19[-indices, ]

#train model
model %>% train(cars_19_input_fn(train, num_epochs = 1000))

#evaluate model
model %>% evaluate(cars_19_input_fn(test))

#predict
yhat <- model %>% predict(cars_19_input_fn(test))

Results are very close to the R closed form estimates:

postResample(yhat, y)
     RMSE  Rsquared       MAE 
2.5583185 0.7891934 1.9381757 

R: SVM to Predict MPG for 2019 Vehicles

Continuing on the below post, I am going to use a support vector machine (SVM) to predict combined miles per gallon for all 2019 motor vehicles.

Part 1: Using Decision Trees and Random Forest to Predict MPG for 2019 Vehicles

Part 2: Using Gradient Boosted Machine to Predict MPG for 2019 Vehicles

The raw data is located on the EPA government site

The variables/features I am using for the models are: Engine displacement (size), number of cylinders, transmission type, number of gears, air inspired method, regenerative braking type, battery capacity Ah, drivetrain, fuel type, cylinder deactivate, and variable valve. 

There are 1253 vehicles in the dataset (does not include pure electric vehicles) summarized below.

fuel_economy_combined    eng_disp        num_cyl       transmission
 Min.   :11.00         Min.   :1.000   Min.   : 3.000   A  :301     
 1st Qu.:19.00         1st Qu.:2.000   1st Qu.: 4.000   AM : 46     
 Median :23.00         Median :3.000   Median : 6.000   AMS: 87     
 Mean   :23.32         Mean   :3.063   Mean   : 5.533   CVT: 50     
 3rd Qu.:26.00         3rd Qu.:3.600   3rd Qu.: 6.000   M  :148     
 Max.   :58.00         Max.   :8.000   Max.   :16.000   SA :555     
                                                        SCV: 66     
   num_gears                      air_aspired_method
 Min.   : 1.000   Naturally Aspirated      :523     
 1st Qu.: 6.000   Other                    :  5     
 Median : 7.000   Supercharged             : 55     
 Mean   : 7.111   Turbocharged             :663     
 3rd Qu.: 8.000   Turbocharged+Supercharged:  7     
 Max.   :10.000                                     
                                                    
                 regen_brake   batt_capacity_ah 
             No        :1194   Min.   : 0.0000  
 Electrical Regen Brake:  57   1st Qu.: 0.0000  
 Hydraulic Regen Brake :   2   Median : 0.0000  
                               Mean   : 0.3618  
                               3rd Qu.: 0.0000  
                               Max.   :20.0000  
                                                
                     drive    cyl_deactivate
 2-Wheel Drive, Front   :345  Y: 172
 2-Wheel Drive, Rear    :345  N:1081
 4-Wheel Drive          :174  
 All Wheel Drive        :349  
 Part-time 4-Wheel Drive: 40  
                              
                              
                                      fuel_type   
 Diesel, ultra low sulfur (15 ppm, maximum): 28           
 Gasoline (Mid Grade Unleaded Recommended) : 16           
 Gasoline (Premium Unleaded Recommended)   :298                 
 Gasoline (Premium Unleaded Required)      :320                 
 Gasoline (Regular Unleaded Recommended)   :591                 
                                                                
                                                                
 variable_valve
 N:  38        
 Y:1215        

Starting with an untuned base model:

set.seed(123)
m_svm_untuned <- svm(formula = fuel_economy_combined ~ .,
                     data    = test)

pred_svm_untuned <- predict(m_svm_untuned, test)

yhat <- pred_svm_untuned
y <- test$fuel_economy_combined
svm_stats_untuned <- postResample(yhat, y)

svm_stats_untuned
     RMSE  Rsquared       MAE 
2.3296249 0.8324886 1.4964907 

Similar to the results for the untuned boosted model.  I am going to run a grid search and tune the support vector machine.

hyper_grid <- expand.grid(
  cost = 2^seq(-5,5,1),
  gamma= 2^seq(-5,5,1)  
)
e <- NULL

for(j in 1:nrow(hyper_grid)){
  set.seed(123)
  m_svm_untuned <- svm(
    formula = fuel_economy_combined ~ .,
    data    = train,
    gamma = hyper_grid$gamma[j],
    cost = hyper_grid$cost[j]
  )  
  
  pred_svm_untuned <-predict(
    m_svm_untuned,
    newdata = test
  )
  
  yhat <- pred_svm_untuned
  y <- test$fuel_economy_combined
  e[j] <- postResample(yhat, y)[1]
  cat(j, "\n")
}

which.min(e)  #minimum MSE

The best tuned support vector machine has a cost of 32 and a gamma of .25.

I am going to run this combination:

set.seed(123)
m_svm_tuned <- svm(
  formula = fuel_economy_combined ~ .,
  data    = test,
  gamma = .25,
  cost = 32,
  scale=TRUE
  )  

pred_svm_tuned <- predict(m_svm_tuned,test)

yhat<-pred_svm_tuned 
y<-test$fuel_economy_combined
svm_stats<-postResample(yhat,y)

svm_stats
     RMSE  Rsquared       MAE 
0.9331948 0.9712492 0.7133039 

The tuned support vector machine outperforms the gradient boosted model substantially with a MSE of .87 vs a MSE of 3.25 for the gradient boosted model and a MSE of 3.67 for the random forest.

summary(m_svm_tuned)

Call:
svm(formula = fuel_economy_combined ~ ., data = test, gamma = 0.25, cost = 32, scale = TRUE)


Parameters:
   SVM-Type:  eps-regression 
 SVM-Kernel:  radial 
       cost:  32 
      gamma:  0.25 
    epsilon:  0.1 


Number of Support Vectors:  232

sum(abs(res)<=1) / 314
[1] 0.8503185  

The model is able to predict 85% of vehicles within 1 MPG of EPA estimate. Considering I am not rounding this is a great result.

The model also does a much better job with outliers as none of the models predicted the Hyundai Ioniq well.

tmp[which(abs(res) > svm_stats[1] * 3), ] #what cars are 3 se residuals
                 Division        Carline fuel_economy_combined pred_svm_tuned
641 HYUNDAI MOTOR COMPANY          Ioniq                    55       49.01012
568                TOYOTA      CAMRY XSE                    26       22.53976
692            Volkswagen Arteon 4Motion                    23       26.45806
984            Volkswagen          Atlas                    19       22.23552

R: Gradient Boosted Machine to Predict MPG for 2019 Vehicles

Continuing on the below post, I am going to use a gradient boosted machine model to predict combined miles per gallon for all 2019 motor vehicles.

Part 1: Using Decision Trees and Random Forest to Predict MPG for 2019 Vehicles

The raw data is located on the EPA government site

The variables/features I am using for the models are: Engine displacement (size), number of cylinders, transmission type, number of gears, air inspired method, regenerative braking type, battery capacity Ah, drivetrain, fuel type, cylinder deactivate, and variable valve. 

There are 1253 vehicles in the dataset (does not include pure electric vehicles) summarized below.

fuel_economy_combined    eng_disp        num_cyl       transmission
 Min.   :11.00         Min.   :1.000   Min.   : 3.000   A  :301     
 1st Qu.:19.00         1st Qu.:2.000   1st Qu.: 4.000   AM : 46     
 Median :23.00         Median :3.000   Median : 6.000   AMS: 87     
 Mean   :23.32         Mean   :3.063   Mean   : 5.533   CVT: 50     
 3rd Qu.:26.00         3rd Qu.:3.600   3rd Qu.: 6.000   M  :148     
 Max.   :58.00         Max.   :8.000   Max.   :16.000   SA :555     
                                                        SCV: 66     
   num_gears                      air_aspired_method
 Min.   : 1.000   Naturally Aspirated      :523     
 1st Qu.: 6.000   Other                    :  5     
 Median : 7.000   Supercharged             : 55     
 Mean   : 7.111   Turbocharged             :663     
 3rd Qu.: 8.000   Turbocharged+Supercharged:  7     
 Max.   :10.000                                     
                                                    
                 regen_brake   batt_capacity_ah 
             No        :1194   Min.   : 0.0000  
 Electrical Regen Brake:  57   1st Qu.: 0.0000  
 Hydraulic Regen Brake :   2   Median : 0.0000  
                               Mean   : 0.3618  
                               3rd Qu.: 0.0000  
                               Max.   :20.0000  
                                                
                     drive    cyl_deactivate
 2-Wheel Drive, Front   :345  Y: 172
 2-Wheel Drive, Rear    :345  N:1081
 4-Wheel Drive          :174  
 All Wheel Drive        :349  
 Part-time 4-Wheel Drive: 40  
                              
                              
                                      fuel_type   
 Diesel, ultra low sulfur (15 ppm, maximum): 28           
 Gasoline (Mid Grade Unleaded Recommended) : 16           
 Gasoline (Premium Unleaded Recommended)   :298                 
 Gasoline (Premium Unleaded Required)      :320                 
 Gasoline (Regular Unleaded Recommended)   :591                 
                                                                
                                                                
 variable_valve
 N:  38        
 Y:1215        

Starting with an untuned base model:

trees <- 1200
m_boosted_reg_untuned <- gbm(
  formula = fuel_economy_combined ~ .,
  data    = train,
  n.trees = trees,
  distribution = "gaussian"
)

> summary(m_boosted_reg_untuned)
                                  var     rel.inf
eng_disp                     eng_disp 41.26273684
batt_capacity_ah     batt_capacity_ah 24.53458898
transmission             transmission 11.33253784
drive                           drive  8.59300859
regen_brake               regen_brake  8.17877824
air_aspired_method air_aspired_method  2.11397865
num_gears                   num_gears  1.90999021
fuel_type                   fuel_type  1.65692562
num_cyl                       num_cyl  0.22260369
variable_valve         variable_valve  0.11043532
cyl_deactivate         cyl_deactivate  0.08441602
> boosted_stats_untuned
     RMSE  Rsquared       MAE 
2.4262643 0.8350367 1.7513331 

The untuned GBM model performs better than the multiple linear regression model, but worse than the random forest.

I am going to tune the GBM by running a grid search:

#create hyperparameter grid
hyper_grid <- expand.grid(
  shrinkage = seq(.07, .12, .01),
  interaction.depth = 1:7,
  optimal_trees = 0,
  min_RMSE = 0
)

#grid search
for (i in 1:nrow(hyper_grid)) {
  set.seed(123)
  gbm.tune <- gbm(
    formula = fuel_economy_combined ~ .,
    data = train_random,
    distribution = "gaussian",
    n.trees = 5000,
    interaction.depth = hyper_grid$interaction.depth[i],
    shrinkage = hyper_grid$shrinkage[i],
  )
  
  hyper_grid$optimal_trees[i] <- which.min(gbm.tune$train.error)
  hyper_grid$min_RMSE[i] <- sqrt(min(gbm.tune$train.error))
  
  cat(i, "\n")
}

The hyper grid is 42 rows which is all combinations of shrinkage and interaction depths specified above.

> head(hyper_grid)
  shrinkage interaction.depth optimal_trees min_RMSE
1      0.07                 1             0        0
2      0.08                 1             0        0
3      0.09                 1             0        0
4      0.10                 1             0        0
5      0.11                 1             0        0
6      0.12                 1             0        0 

After running the grid search, it is apparent that there is overfitting. This is something to be very careful about.  I am going to run a 5 fold cross validation to estimate out of bag error vs MSE.  After running the 5 fold CV, this is the best model that does not overfit:

> m_boosted_reg <- gbm(
  formula = fuel_economy_combined ~ .,
  data    = train,
  n.trees = trees,
  distribution = "gaussian",
  shrinkage = .09,
  cv.folds = 5,
  interaction.depth = 5
)

best.iter <- gbm.perf(m_boosted_reg, method = "cv")
pred_boosted_reg_ <- predict(m_boosted_reg,n.trees=1183, newdata = test)
mse_boosted_reg_ <- RMSE(pred = pred_boosted_reg, obs = test$fuel_economy_combined) ^2
boosted_stats<-postResample(pred_boosted_reg,test$fuel_economy_combined)

The fitted black curve above is MSE and the fitted green curve is the out of bag estimated error.  1183 is the optimal amount of iterations.

> pred_boosted_reg <- predict(m_boosted_reg,n.trees=1183, newdata = test)
> mse_boosted_reg <- RMSE(pred = pred_boosted_reg, obs = test$fuel_economy_combined) ^2
> boosted_stats<-postResample(pred_boosted_reg,test$fuel_economy_combined)
> boosted_stats
     RMSE  Rsquared       MAE 
1.8018793 0.9092727 1.3334459 
> mse_boosted_reg
3.246769 

The tuned gradient boosted model performs better than the random forest with a MSE of 3.25 vs 3.67 for the random forest.

> summary(res)
    Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
-5.40000 -0.90000  0.00000  0.07643  1.10000  9.10000 

50% of the predictions are within 1 MPG of the EPA Government Estimate.

The largest residuals are exotics and a hybrid which are the more unique data points in the dataset. 

> tmp[which(abs(res) > boosted_stats[1] * 3), ] 
                  Division            Carline fuel_economy_combined pred_boosted_reg
642  HYUNDAI MOTOR COMPANY         Ioniq Blue                    58             48.5
482 KIA MOTORS CORPORATION           Forte FE                    35             28.7
39             Lamborghini    Aventador Coupe                    11             17.2
40             Lamborghini Aventador Roadster                    11             17.2

R: MLR, Decision Trees and Random Forest to Predict MPG for 2019 Vehicles

I am going to use regression, decision trees, and the random forest algorithm to predict combined miles per gallon for all 2019 motor vehicles.  The raw data is located on the EPA government site

After preliminary diagnostics, exploration and cleaning I am going to start with a multiple linear regression model.

The variables/features I am using for the models are: Engine displacement (size), number of cylinders, transmission type, number of gears, air inspired method, regenerative braking type, battery capacity Ah, drivetrain, fuel type, cylinder deactivate, and variable valve. 

There are 1253 vehicles in the dataset (does not include pure electric vehicles) summarized below.

fuel_economy_combined    eng_disp        num_cyl       transmission
 Min.   :11.00         Min.   :1.000   Min.   : 3.000   A  :301     
 1st Qu.:19.00         1st Qu.:2.000   1st Qu.: 4.000   AM : 46     
 Median :23.00         Median :3.000   Median : 6.000   AMS: 87     
 Mean   :23.32         Mean   :3.063   Mean   : 5.533   CVT: 50     
 3rd Qu.:26.00         3rd Qu.:3.600   3rd Qu.: 6.000   M  :148     
 Max.   :58.00         Max.   :8.000   Max.   :16.000   SA :555     
                                                        SCV: 66     
   num_gears                      air_aspired_method
 Min.   : 1.000   Naturally Aspirated      :523     
 1st Qu.: 6.000   Other                    :  5     
 Median : 7.000   Supercharged             : 55     
 Mean   : 7.111   Turbocharged             :663     
 3rd Qu.: 8.000   Turbocharged+Supercharged:  7     
 Max.   :10.000                                     
                                                    
                 regen_brake   batt_capacity_ah 
             No        :1194   Min.   : 0.0000  
 Electrical Regen Brake:  57   1st Qu.: 0.0000  
 Hydraulic Regen Brake :   2   Median : 0.0000  
                               Mean   : 0.3618  
                               3rd Qu.: 0.0000  
                               Max.   :20.0000  
                                                
                     drive    cyl_deactivate
 2-Wheel Drive, Front   :345  Y: 172
 2-Wheel Drive, Rear    :345  N:1081
 4-Wheel Drive          :174  
 All Wheel Drive        :349  
 Part-time 4-Wheel Drive: 40  
                              
                              
                                      fuel_type   
 Diesel, ultra low sulfur (15 ppm, maximum): 28           
 Gasoline (Mid Grade Unleaded Recommended) : 16           
 Gasoline (Premium Unleaded Recommended)   :298                 
 Gasoline (Premium Unleaded Required)      :320                 
 Gasoline (Regular Unleaded Recommended)   :591                 
                                                                
                                                                
 variable_valve
 N:  38        
 Y:1215        

Call:
lm(formula = fuel_economy_combined ~ eng_disp + transmission + 
    num_gears + air_aspired_method + regen_brake + batt_capacity_ah + 
    drive + fuel_type + cyl_deactivate + variable_valve, data = cars_19)

Residuals:
     Min       1Q   Median       3Q      Max 
-12.7880  -1.6012   0.1102   1.6116  17.3181 

Coefficients:
                                                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)                                        36.05642    0.82585  43.660  < 2e-16 ***
eng_disp                                           -2.79257    0.08579 -32.550  < 2e-16 ***
transmissionAM                                      2.74053    0.44727   6.127 1.20e-09 ***
transmissionAMS                                     0.73943    0.34554   2.140 0.032560 *  
transmissionCVT                                     6.83932    0.62652  10.916  < 2e-16 ***
transmissionM                                       1.08359    0.31706   3.418 0.000652 ***
transmissionSA                                      0.63231    0.22435   2.818 0.004903 ** 
transmissionSCV                                     2.73768    0.40176   6.814 1.48e-11 ***
num_gears                                           0.21496    0.07389   2.909 0.003691 ** 
air_aspired_methodOther                            -2.70781    1.99491  -1.357 0.174916    
air_aspired_methodSupercharged                     -1.62171    0.42210  -3.842 0.000128 ***
air_aspired_methodTurbocharged                     -1.79047    0.22084  -8.107 1.24e-15 ***
air_aspired_methodTurbocharged+Supercharged        -1.68028    1.04031  -1.615 0.106532    
regen_brakeElectrical Regen Brake                  12.59523    0.90030  13.990  < 2e-16 ***
regen_brakeHydraulic Regen Brake                    6.69040    1.94379   3.442 0.000597 ***
batt_capacity_ah                                   -0.47689    0.11838  -4.028 5.96e-05 ***
drive2-Wheel Drive, Rear                           -2.54806    0.24756 -10.293  < 2e-16 ***
drive4-Wheel Drive                                 -3.14862    0.29649 -10.620  < 2e-16 ***
driveAll Wheel Drive                               -3.12875    0.22300 -14.030  < 2e-16 ***
drivePart-time 4-Wheel Drive                       -3.94765    0.46909  -8.415  < 2e-16 ***
fuel_typeGasoline (Mid Grade Unleaded Recommended) -5.54594    0.97450  -5.691 1.58e-08 ***
fuel_typeGasoline (Premium Unleaded Recommended)   -5.44412    0.70009  -7.776 1.57e-14 ***
fuel_typeGasoline (Premium Unleaded Required)      -6.01955    0.70542  -8.533  < 2e-16 ***
fuel_typeGasoline (Regular Unleaded Recommended)   -6.43743    0.68767  -9.361  < 2e-16 ***
cyl_deactivateY                                     0.52100    0.27109   1.922 0.054851 .  
variable_valveY                                     2.00533    0.59508   3.370 0.000775 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

  standard error: 2.608 on 1227 degrees of freedom
Multiple R-squared:  0.8104,    Adjusted R-squared:  0.8066 
F-statistic: 209.8 on 25 and 1227 DF,  p-value: < 2.2e-16 

The fitted MSE is 6.8 and predicted MSE of 6.83.  Some of the below residuals are too large.  The extreme large residual is a Hyundai Ioniq which none of the models predict very well as it is unique vehicle (versus the other data points).

Let's try a decision tree regression model.

#regression tree full
m_reg_tree_full <- rpart(formula = fuel_economy_combined ~ .,
                         data    = train,
                         method  = "anova",)
#regression tree tuned
m_reg_tree_trimmed <- rpart(
  formula = fuel_economy_combined ~ .,
  data    = train,
  method  = "anova",
  control = list(minsplit = 10, cp = .0005)
)

#rpart.plot(m_reg_tree_full)
plotcp(m_reg_tree_full)

pred_decision_tree_full <- predict(m_reg_tree_full, newdata = test)
mse_tree_full <- RMSE(pred = pred_decision_tree_full, obs = test$fuel_economy_combined) ^2

pred_decision_tree_trimmed <- predict(m_reg_tree_trimmed, newdata = test)
mse_tree_trimmed <- RMSE(pred = pred_decision_tree_trimmed, obs = test$fuel_economy_combined) ^2
plotcp(m_reg_tree_trimmed)

After tuning the decision tree the predicted MSE is 6.20 which is better than the regression model.

Finally let's try a random forest model.  The random forest should produce the best model as it will attempt to remove some of the correlation within the decision tree structure.

#random forest
m_random_forest_full <-randomForest(formula = fuel_economy_combined ~ ., data = train)
predict_random_forest_full <- predict(m_random_forest_full, newdata = test)
mse_random_forest_full <- RMSE(pred = predict_random_forest_full, obs = test$fuel_economy_combined) ^ 2

which.min(m_random_forest_full$mse)

#random forest tuned
m_random_forest <- randomForest(formula = fuel_economy_combined ~ ., data = train, ntree = 250)
plot(m_random_forest)
predict_random_forest <- predict(m_random_forest, newdata = test)
mse_random_forest <- RMSE(pred = predict_random_forest, obs = test$fuel_economy_combined) ^ 2

plot(tmp$test.fuel_economy_combined - tmp$r.predict_random_forrest., ylab = "residuals",main = "Random Forest")

varImpPlot(m_random_forest)

The error stabilizes at 250 trees.  randomForest() by default uses 500 trees which is unnecessary.

After tuning the random forest the model has the lowest fitted and predicted MSE of 3.67 which is substantially better than the MSE of the decision tree 6.2

The random forest also has an r-squared of .9

Engine size, number of cylinders, and transmission type are the largest contributors to accuracy.

R: Birthday Problem

An interesting and classic probability question is the birthday problem.

The birthday problem asks how many individuals are required to be in one location so there is a probability of 50% that at least two individuals in the group have the same birthday.

To solve:

If there are just 23 people in one location there is a 50.7% probability there will be at least one pair with the same birthday.

R: K-Means Clustering MLB Data

k-means clustering is a useful unsupervised learning data mining tool for assigning n observations into k groups which allows a practitioner to segment a dataset.

I play in a fantasy baseball league and using five offensive variables (R, AVG, HR, RBI, SB) I am going to use k-means clustering to:

1) Determine how many coherent groups there are in major league baseball. For example,

is there a power and high average group? Is there a low power, high average, and speed group?

2) Assign players to these groups to determine which players are similar or can act as replacements. I am not using this algorithm to predict how players will perform in 2017.

For a data source I am going to use all MLB offensive players in 2016 which had at least 400 plate appearances from http://www.baseball-reference.com This dataset has n= 256 players.

Sample data below

Step 1

How many k groups should I use?

The within groups sum of squares plot below suggests k=7 groups is ideal. k=9 is too many groups for n=256 and the silhouette plot for k=9 is poor.

Step 2

Is k=7 groups a good solution?

Let's look at a silhouette plot to look at the fit of each cluster and the overall k=7 clusters.

The average silhouette width = .64 indicates a reasonable structure has been found. Cluster 4 which is the speed group has a low silhouette width of .37. I am OK with this as it is the smallest group and speed is the hardest offensive tool to find in MLB.

Step 3

Calculate group means for k=7 groups

 

Players that are classified in cluster 3 are the elite players in MLB. Based on 2016 stats, 31 players make up cluster 3. On average they have the highest AVG, R, RBI, HR, and the second highest SB. 

Adding Hampel Psi Function to robustreg

I am currently working on adding the Hampel psi function to robustreg.

Pure R implementation:

psiHampel <- function(r, a, b, c) {
    psi <- NULL
    for (i in 1:length(r)) {
        if (abs(r[i]) <= a) {
            psi[i] <- r[i]
        } else if (abs(r[i]) > a & abs(r[i]) <= b) {
            psi[i] <- a * sign(r[i])
        } else if (abs(r[i]) > b & abs(r[i]) <= c) {
            psi[i] <- (a * (c - abs(r[i]))/(c - b)) * sign(r[i])
        } else {
            psi[i] <- 0
        }
    }
    return(psi)
}

Rcpp/C++ implementation:

#include <Rcpp.h>
#include <math.h>
using namespace Rcpp;
using namespace std;

// [[Rcpp::export]]
NumericVector psiHampel_rcpp(NumericVector r, double a, double b, double c)
{
    int n = r.size();
    NumericVector y = clone(r);

    for (int i = 0; i < n; i++) {
        if (abs(r[i]) <= a) {
            y[i] = r[i];
        }
        else if (
            abs(r[i]) > a && abs(r[i]) <= b) {
            if (r[i] > 0) {
                y[i] = a;
            }
            else {
                y[i] = -a;
            }
        }
        else if (
            abs(r[i]) > b && abs(r[i]) <= c) {
            if (r[i] > 0) {
                y[i] = (a * (c - abs(r[i])) / (c - b));
            }
            else {
                y[i] = (a * (c - abs(r[i])) / (c - b) * -1);
            }
        }
        else {
            y[i] = 0;
        }
    }
    return y;
}

Below is a ggplot2 graph of values a=2, b=4, c=8 where x ranges from -10 to 10:

z=seq(-50,50,.01)
all.equal(psiHampel(z,2,4,8), psiHampel_rcpp(z,2,4,8))
[1] TRUE

Both functions have the same result although the C++ implementation is much faster.

R: Baseball Pitching Wins Above Replacement and Salary

Are elite baseball pitchers worth their salaries? To investigate this I fitted linear and robust linear models using Baseball-Reference.com definition of wins above replacement. The universe of data is all pitchers in the year 2015 who started at least 20 games or as a reliever pitched 70 outs which is 298 players.

The distribution of war is below:

 Min.      1st Qu. Median Mean    3rd Qu. Max.
-1.79      0.2125  0.95      1.219   1.905     9.28

standard dev: 1.61
mad:  1.245

Fitting a linear model to the data:

We can see that there is a linear relationship between salary and war as salary is significant.  The correlation between the two variables is ~.28 but the MSE is 2.4 which indicates the model isn't the best fit.  The linear model suggests that each additional $11,883,599 in player salary should buy a win over a replacement player.

Investigating a robust model:

The robust model is a better fit as MSE is significantly lower at 1.47.  The correlation between salary and war is slightly lower at .277.  The advantage of a robust model is it will minimize outliers by assigning lower weights.  The robust model suggests that each additional $14,065,063 in player salary should buy a win over a replacement player.



Below is a table of 2015 war, 2015 salary, and the upper prediction interval of war based on 2015 salary:

The top ten pitchers in 2015 all had better seasons than the upper end of the prediction interval based on their salary.